This unit we dealt with power and the different forms of energy. We learned exactly what energy is and observed the ways in which it plays a role in a system and transfers from one account to another.
Worksheet 1a and 1b: Pie Charts
In this worksheet we observed several different situations in which energy is developed and transferred over the course of an objects movement. We started off learning the different types of energy in the form of a bank analogy. When one goes to a bank, there is the option of either withdrawing money or putting it in a savings account, this situation also applies to energy as it is transferred, and stored over time
Energy is the ability to cause change
Although we briefly discussed the forms of energy release, we have put our main focus into the energy that is stored:
Chemical Energy: this is the energy stored in bonds of chemical compounds often in the form of heat that is broken or burned such as particles in food or the body
Elastic Energy: this is the energy that is stored in a rope, bungee, or spring, or it occurs when there is some displacement
Electrical Energy: this is the energy that moves through a wire or another appliance
Gravitational Energy: this is the energy an object possesses due to its position on the gravitational field
Dissipated Energy: this is energy that has been transformed from some initial form to a final form that can no longer be used
Our first application with these energy forms came with the use of pie charts. We were given several different scenarios and using 3 or more pie charts, we had to describe what the energy was doing in each point in time.
This scenario displays a wind up toy at rest. There is no movement, but because the spring is wound up inside of the toy, there is nothing but elastic energy
Now the toy is not only wound up but moving at a constant speed up a hill. Because the toy is in motion and wound up, there is both elastic energy and kinetic energy in the beginning, as it moves up the hill, the kinetic energy stays the same because kinetic energy always remains constant throughout the system, but the elastic energy decreases and gravitational energy comes into play. When it reaches the highest point on the hill, the elastic energy is totally gone and there is nothing but gravitational and kinetic energy left
This situation is different because the toy is now coming to a stop. It starts off wound up and moving so there is kinetic and elastic energy, it starts to slow down so the kinetic and elastic energy decreases and dissipated energy comes in. In the final bubble, there is all dissipated energy because the toy is stopped

This situation is more complex as there are various different stages of energy that need to be expressed. At point A the ball is barely above the ground but it is in motion, so there is a little gravitational energy but mostly kinetic energy. At point B the ball is higher off the ground so there is more gravitational energy but also kinetic energy. Point C has the most gravitational energy because it is at the highest point, and the rest of the space is kinetic energy. Point D is halfway to the highest point, so it was designated with half kinetic and half gravitational energy. Finally, Point E is at the same height as Point A, so it has the same kinetic and gravitational energy

In this situation, a car driving down the street is operated by a motor which is chemical energy as well as kinetic energy. With previous knowledge of how gas is burned over time, the second bubble still has the same amount of kinetic energy, but the chemical energy has shrunk and been replaced with dissipated energy which represents the decrease of gas after a period of time. Finally, in the last bubble, the kinetic energy is still the same, there is a little bit of chemical energy left, and the rest is dissipated energy
Worksheet 2: Hooke’s Law and Elastic Energy
In this worksheet we learned more about elastic energy and discovered 2 ways to solve for it in the unit of joules which is equivalent to a Newton-Meter. We also learned an equation that we ca use to solve for force using two variables that will be described later.
The first way to solve for elastic energy is by finding the area under the curve on a graph the same method we used to solve for acceleration. Using either (base)(height) for rectangles, (1/2)(base)(height) for triangles, or both, you can find the elastic energy within a system.
For the following problems we were given a distance the spring was stretched, and then using that distance, we formed the needed triangle/rectangle to calculate the area.
Using the graph above, this problem designates that the spring is stretched from 0 to 10 cm which is marked off in blue. Two small triangles and one rectangle can be formed within the larger triangle, and those values are then plugged into the formulas as shown to get 5 newton-meters or Joules
This time the spring is stretched from 15 to 25 cm marked off in green. One rectangle and one triangle can be formed within this and the values are plugged into the formulas as shown to get 20 newton-meters or Joules
The second way to solve for elastic energy is by using the formula: 1/2kx^2.
The K stands for the spring constant which is representative of the force exerted on a spring/rope/etc. to stretch or compress it. The spring constant is directly proportional to how stiff the spring is, and when looking on a graph, the spring constant is representative of the slope, therefore, if the spring constant is not given in a problem, it can be easily found using the slope of the line. The units for K are newtons per meter (N/m) The x is simply the length the spring is stretched or compressed.
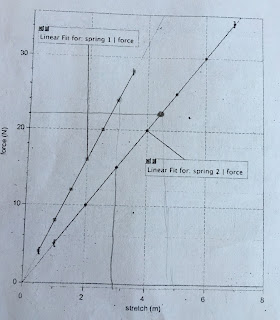
2. 3. The graph and photo below shows 2 lines and the ways in which I calculated the spring constant using the slope formula for each line
The next problem requires you to use one of the spring constants that was calculated to find the elastic energy using the formula Eelastic=1/2kx^2 and simply plugging the values in
The following problem taught us an equation that can be used to solve for force, the spring constant, or the amount the spring was stretched or compressed if necessary. The formula is: F=Kx, and it is easy to use, one just must remember that the x value must always be in meters. An example problem is shown below
Worksheet 3: Qualitative Energy Storage and Conversion with Bar Graphs
This worksheet was like a continuation of the pie graphs, only this time, the energy is represented in a different form. In these scenarios, energy in a system was displayed on bar graphs. There is one graph for the energy working on the object in Position A, or before, and another graph for the energy working on the object in Position B, or after. There is a circle in between both graphs in which you write all of the objects that are considered within the system
Before a few examples are shown, there are a few rules that are necessary to remember when designing these bar graphs.
RULES:
- Energy before ALWAYS EQUALS energy after, so there will always be the same amount of energy in a system no matter what
- Because energy before=energy after, the amount of bars chosen to be displayed on each graph must be the same, so if there are 5 boxes on graph A, there must be 5 boxes on graph B
- When gravitational energy comes into play, the amount of boxes designated is directly related to the height of the object, and therefore, if there are several questions that are based upon one another and the height is the same for all of them, the amount of boxes for gravitational energy must also be the same
- If friction is designated as a factor, there will be dissipated energy, also called thermal energy on these graphs, if there is no friction, there will be no dissipated energy
- If the problem removes a certain object from a system, then the role they play in the scenario becomes something called WORK which is defined as a force applied to an object to move it. Work is always outside of the system
- Kinetic energy relates to how fast something is going, gravitational energy is related to the height of an object, and dissipated energy represent an energy transfer
This is a very basic problem that designates all the objects within the system. In position A the cart is at rest on the spring which is shown on the graph having 5 blocks of elastic energy. In position B, the cart has moved around the track and now has some kinetic energy as well as gravitational energy. Notice there are still 5 boxes on B’s graph, but 3 went to gravitational and 2 to kinetic. The Qualitative Energy Conservation Equation is the written form of all the energy
present in graph A and B, so for this instance, the equation is Eelastic= Ekinetic+Egravitational
This problem is a continuation of the previous problem and gives us as chance to apply some of the rules. This time, the spring is not a part of the system, which means that it is applying work to the cart outside the system. Because of this, there will be no blocks on graph A, but there will be a Work arrow with “5 blocks” on the outside of the circle as shown, and graph B will look the same as before with the same amount of gravitational blocks because the cart is at the same height. This time, the energy conservation equation is Work= Ekinetic+Egravitational

This problem is yet again another continuation of the first problem but the spring returns to the system and there is now friction on the track. There is still the same amount of elastic energy on graph A, but since there is friction, there will be some dissipated energy. There must be 3 blocks of gravitational energy just like the previous 2 problems because once again, the cart remains at the same height, so the remaining 2 blocks must be divided between dissipated and kinetic, and a triangle represents a half block, so kinetic got one and a half blocks and dissipated got a half. The qualitative energy conservation equation for this problem is Eelastic= Ekinetic+Egravitational+Edissipated
The following 2 problems are quite similar to the first three, but this time a legend is given that helps when deciding which energy forms to use.
The bungee jumper is standing on the top of the platform and the legend indicates that hA>0 which means that the height of the person is greater than 0, therefore there is gravitational energy. The legend also says vA=0 which means there is no velocity, so that eliminates kinetic energy, and the bungee hasn't yet come into play so there is no elastic energy, leaving all 5 blocks to gravitational. In position B, the legend still says that hB>0, so we know there is still some gravitational energy, the person has stopped bouncing so the vB=0 so no kinetic energy, but the person is hanging from the bungee so there is elastic energy. 2 blocks were assigned to gravitational and 3 to elastic, and the equation is Eg=Eel+Eg

In this problem the bungee is not a part of the system which means that it performs work on the person after he has jumped. The legend still indicates height is greater than 0 and velocity=0, so there is still only gravitational energy in graph A, but for graph B, only 2 blocks of gravitational energy appear like the first problem, and the rest of the work from the bungee is shown coming from the circle with 3 blocks of energy to fill the space which makes the equation Eg= W+Eg
Worksheet 4: Quantitative Energy Calculations and Energy Conservation
Leading into this worksheet we learned 2 new formulas for kinetic and gravitational energy to go along with the elastic equation.
Kinetic Energy=1/2(mass)(velocity)^2
Gravitational Energy=(mass)(gravitational constant)(height)
These equations are pretty straightforward but it is important to remember the units:
mass in kg
velocity in m/s
gravitational constant: 10
height in meters
Anything outside these units must be converted
This is a basic kinetic energy problem that provides the values to be plugged into the formula. It does require you to make a conversion from miles per hour to meters per second by using the values given in the problem and setting up a proportion but aside from that it is a plug and chug
These problems use the gravitational energy equation and provides the height and the mass of the book. The gravitational constant is always going to be 10 because it is the strength of the gravitational field
An illustration of the situation is below
For this problem, you simply plug in 3 and 10, and the height of the book is going to be 0. Even though it would seem as if it were at a certain height because it is not resting on the floor, of not designated at a certain height, it can be assumed that the tabletop represents a height of 0
This problem is completed the same way except this time the height is .68 meters below the book, which would be designated as a negative value in the equation
The final problem is also the same but the height is 2.5 meters above the book so the height value is positive
The following couple of problems allow us to use the same energy bar graphs along with the new formulas we learned for kinetic, elastic, and gravitational energy to actually find quantitative values for this energy. All of these problems are based on the Quantitative Energy Conservation Equation, so it is crucial that that element of the problem is correct before solving for anything else.
This problem starts of providing a scenario with a cart in motion and finishing stopped on a spring. Above the picture it provides the mass, velocity before and after, and the k constant for the problem. The graphs were pretty self explanatory starting off with all kinetic energy and finishing with all elastic energy
The conservation equation for the problem is Ek=Eel, and to the side I have written the formula for each which are the values I will be looking for. Because Ek and Eel are set equal to each other, I know that by solving all of Ek, I have also solved for all of Eel. The question asks for the maximum compression of the spring which is the x value in the elastic formula.After I solved for kinetic energy which was 100 Joules, I set that equal to the elastic energy equation plugging in the 50 k value that was given which leaves only x^2 to solve for. After plugging everything in and making some calculations, we come to the x value of 2m.

This problem brings work back into play as it describes a magnetic rail gun that shoots items into moon orbit, but the rail gun is not a part of the system, which is why the work arrow from the rail gun is going into the circle. On graph B after the items are in orbit, there is nothing but kinetic and gravitational energy, so the conservation equation is W= Ek+Eg. We are given all the values to plug into the formulas, and all that is needed is to convert 100 km to m and the rest is plug and chug to get something along the lines of 1.61x10^10 J
Worksheet 5: Energy Transfer and Power
In this worksheet we learned all about power, what it means, and how to solve for it by once again using energy bar graphs. We also performed a lot of conversions and learned a couple new formulas.
Power is the rate of doing work or the amount of energy consumed per unit of time round in Joules per second also known as a Watt
The equation for power is equal to energy transfer/ time, and that energy transfer can be in the form of kinetic, elastic, gravitational, or any other energy form we have learned. It is quite easy to use as you just put the energy equation on top and divide it by the time it took to do it.
This problem is a simple power problem using the gravitational energy formula over time. It asks you to compare the power between Hulky and Bulky, and Hulky ended up having the most power because although he lifted a lighter weight, he did it in a faster time. The work is shown below
This problem helps us to look at power in a different way. Instead of giving the typical values needed to solve for kinetic energy, this problem gives newtons, mass, and velocity, and although it may not seem like enough it is exactly what we need if we manipulate the formula.
One watt is equal to a Joule per second, and one Joule is equal to a Newton-Meter per second, which can be rewritten as (newtons)(meters per second). Fortunately, a newton is equal to force, and meters per second is equal to the velocity, so we are left with (force)(velocity) and we are given 270N and 25m/s. When those two are multiplied, we are left with 6750 Watts, and divide that by 746 or set up a proportion to get that value in horsepower
One of the final concepts we went over was kilowatt-hours. 1 kilowatt is equal to 1000 watts and there are 3600 seconds in an hour, so in order to convert this into joules, we need to do a conversion, putting the units that need to cancel on the bottom and the units needed on top to eventually get joules
From previous problems we know that power=change in energy/time, but we can rearrange that formula to get change in energy= (power)(time). Since we are looking for kilowatts and we were given watts and hours, we can simply use this formula butch change the watts into kilowatts by moving the decimal three places to the left
Finally, this energy bar graph is just like all the others except this one incorporates the formula for work.
Work=(force)(change in x)
The problem gives us a force in newtons along with a displacement and a mass and is looking for velocity. Using the energy bar graphs we have work coming in from the rifle and kinetic energy resulting, so the equation is W= Ek. Using the force and length of the barrel changed to meters for the work formula and long with the mass for the kinetic energy formula, I solved for velocity